西方经济学03企业生产与成本

企业主要包括个人独资企业、合伙制企业和公司三种类型
生产函数表示在一定时期内在给定的技术条件下，生产中所使用的各种生产要素的数量与所能生产的最大产量之间的关系
一般生产函数表示为

$$Q=f(L,K)$$

生产的短期指生产者来不及调整全部生产要素的数量，至少
有一种生产要素的数量是固定不变的生产周期。
生产的长期指生产者可以调整全部生产要素的生产周期

短期生产函数

假定资本投入量是固定的，以$\overline{K}$表示，劳动投入量是可变的．以$L$表示，则生产函数可以写成

$$Q=f(L,\overline{K})$$

劳动的总产量$TP_L$ 表示与可变要素劳动的每一投入数量相对应的最大总产量

$$TP_L=g(L,\overline{K})$$

劳动的平均产量$AP_L$ 表示平均每一单位可变要素劳动的投入量所生产的产量。其定义公式为

$$AP_L=\frac{TP_L(L,\overline{K})}{L}$$

劳动的边际产量$MP_L$表示增加一单位可变要素劳动的投入量所增加的产量

$$MP_L=\frac{\Delta TP_L(L,\overline{K})}{\Delta L }$$

资本总产量、平均产量、边际产量的定义类似
边际报酬递减：在技术水平和其他因素不变的条件下，在连续等量地将某一种可变生产要素投入增加到其他一种或几种数量固定不变的生产要素上去的过程中，该可变要素的边际产量先是递增的，在这种可变要素的投入量增加到一定数量之后，其边际产量便是递减的了
其三大附加条件：

1. 生产技术水平保持不变，才成立
2. 只有在其他生产要素投入数量不变的条件下才成立
3. 边际产量递减在可变要素投入增加到一定程度后才会出现

总产量 平均产量 边际产量之间的关系

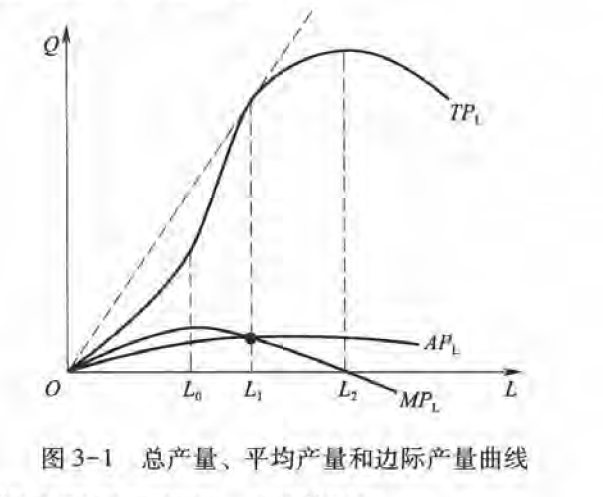
• 在边际报酬递减规律的作用下，劳动的边际产量曲线呈现先增加后递减的趋势
• 相应于边际产量先增加后递减以及边际产扯由正值转为负值，总生产曲线也会呈现出先增加后递减的趋势
• 对应于上述总产量曲线，劳动的平均产益曲线是先增加后递减的。
• 边际产匮曲线与平均产量曲线相交，并且交于平均产矗曲线的最大值点。
  
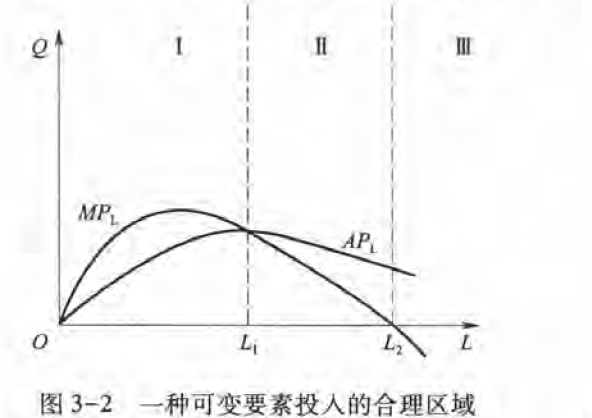
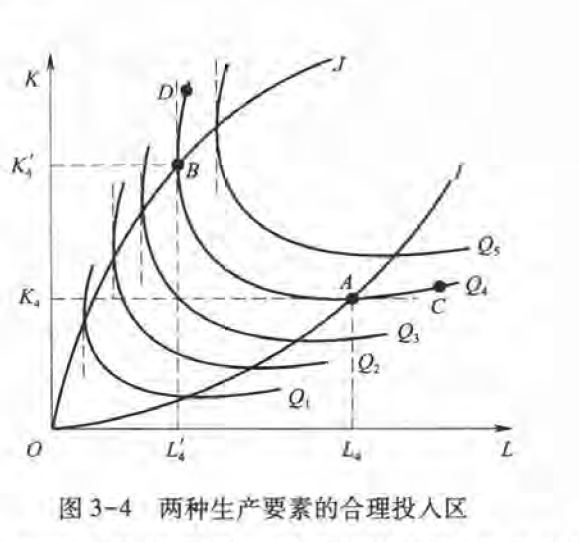
  阶段二是可变资源投入的合理区间

长期生产函数

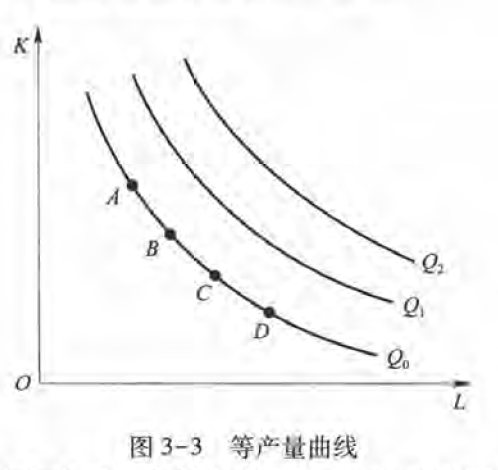
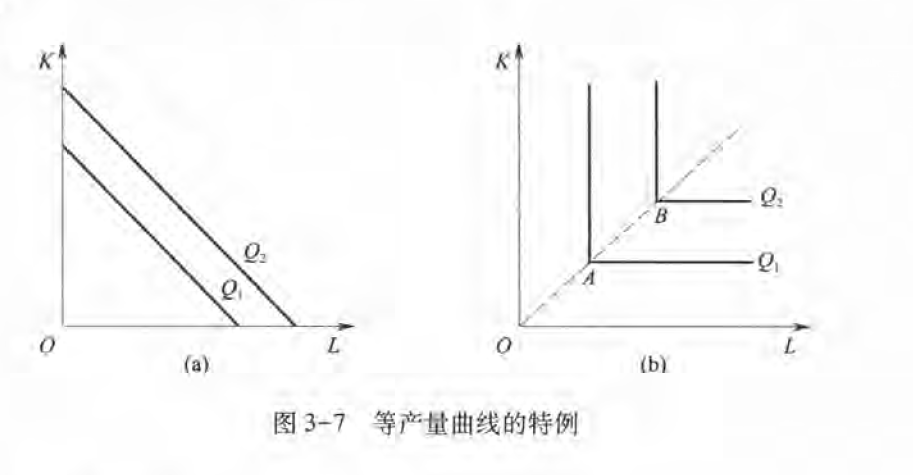
等产量曲线，类似于无差异曲线

边际技术替代率

劳动$L$对资本$K$的边际替代率

$$MRTS_{L,K}=-\frac{\Delta K}{\Delta L}$$

$$MP_L \cdot \Delta L+MP_K \cdot \Delta K\Rightarrow MRTS_{L,K}=-\frac{\Delta K}{\Delta L}=\frac{MP_L}{MP_K}$$

劳动这一生产要素对另外一种生产要素资本的边际技术替代率与劳动的边际产量成正比．与资本的边际产裁成反比。直观上，劳动的企业的生产和成本“生产能力”越强，它就越容易替代资本，劳动对资本的边际技术替代率就越大；相反．如果资本的“生产能力”越强，劳动就越不容易替代资本，劳动对资本的边际技术替代率就越小。

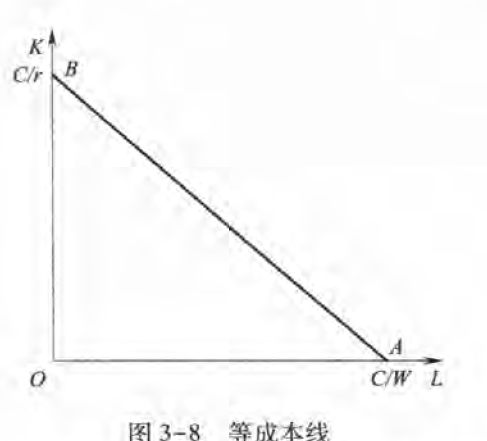
等生产线

假定企业只使用劳动和资本两种生产要素，它们的价格分别为$W$和$r$,则企业在一定时期内投人劳动$L$和租用资本$K$所花费的成本$C$可以表示为：

$$C=WL+rK$$

成本既定条件下产量最大化

$$\begin{align} MRTS_{L,K}=\frac{W}{r} \\ WL+rK=C \end{align}$$

只有当从生产技术角度衡储的劳动对资本的替代率与按市场价格衡扯的二者之间的替代率相等时，企业才能在既定的成本条件下生产出最大的产量，才能使得两种要素投入比例达到最优，企业才能处于生产者均衡状态。

$$\begin{align} \frac{MP_L}{W}=\frac{MP_k}{r} \\ WL+rK=C \end{align}$$

每单位成本购买任意一种生产要素所得到的边际产量都相
等。企业才能在成本既定条件下生产出最大产量

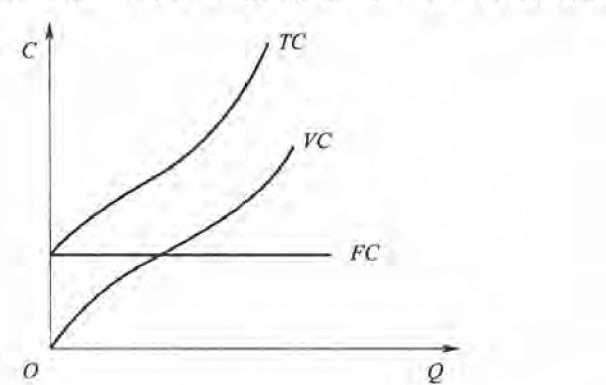
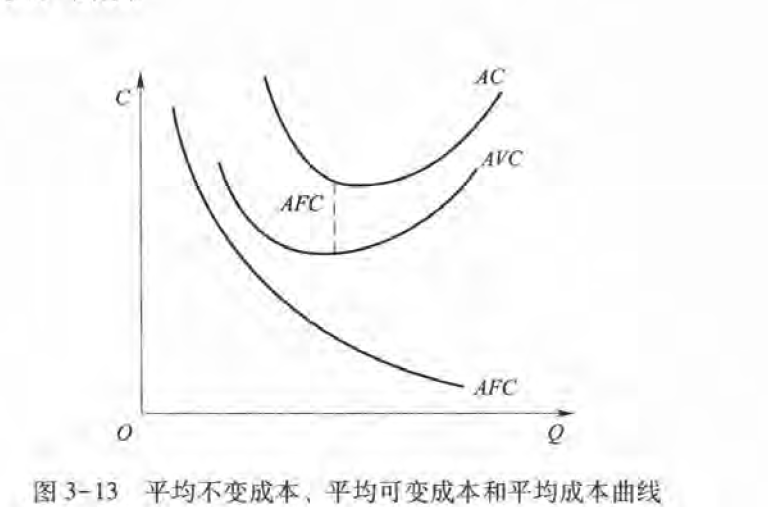
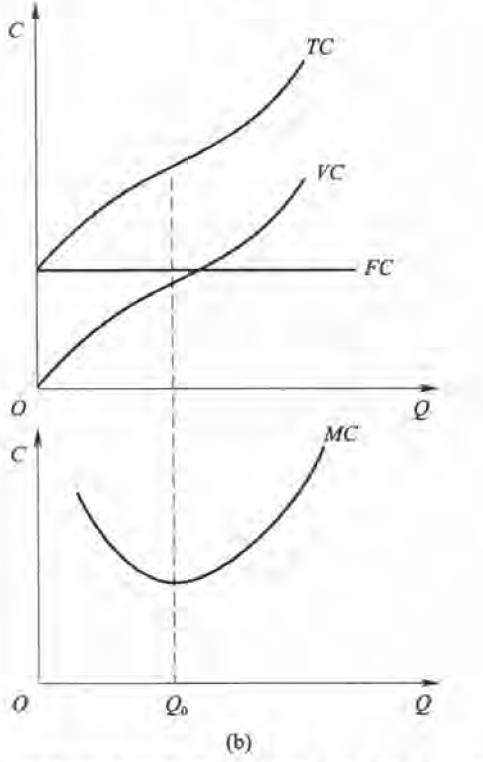
短期成本

TC为总成本，FC为不变成本，VC为可变成本

$$TC=FC+VC$$

$$AC=\frac{TC}{Q} \quad AFC=\frac{FC}{Q} \quad AVC=\frac{VC}{Q}$$

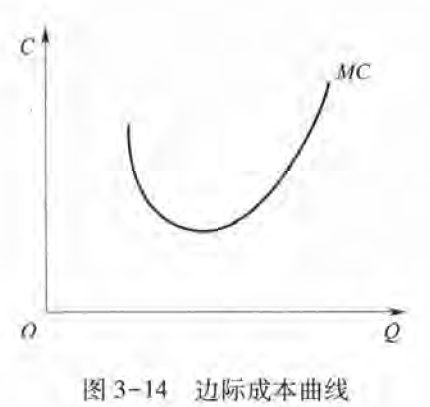
边际成本：

$$MC=\frac{\Delta VC}{\Delta Q}$$

$$AVC=\frac{VC}{Q}=\frac{WL}{Q}=\frac{W}{Q/L}=\frac{W}{AP_L}$$

$$MC=\frac{\Delta VC}{\Delta Q}=\frac{\Delta WL}{\Delta Q}=\frac{\Delta W}{\Delta Q/\Delta L}=\frac{W}{MP_L}$$

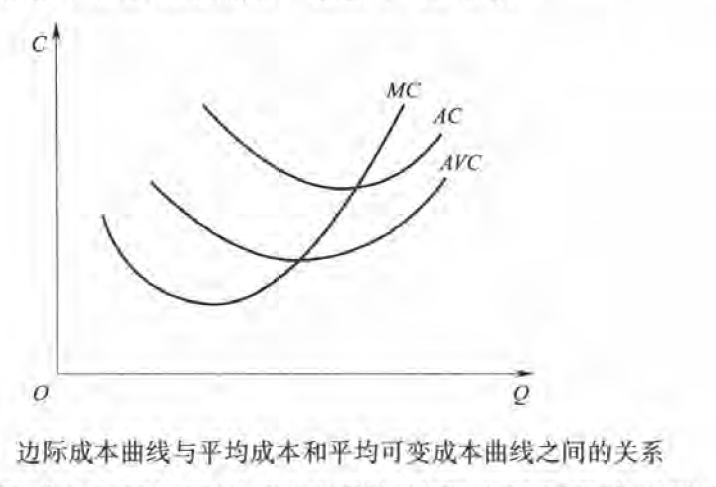
MC与AC AVC相交于其极小值点

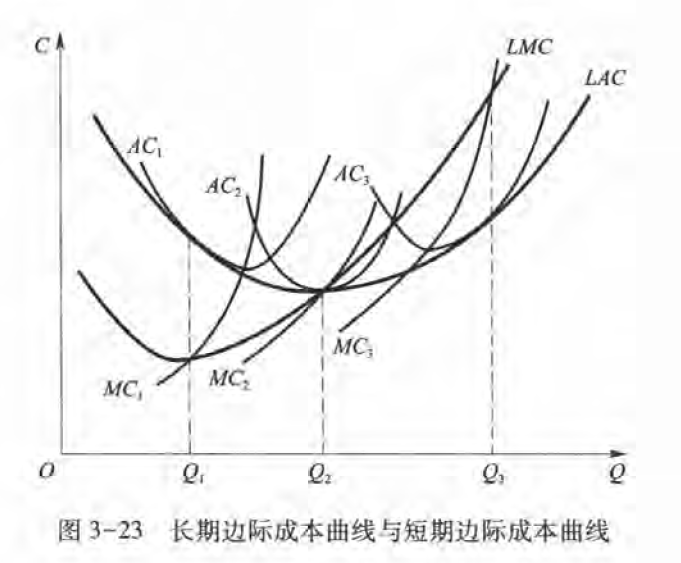
长期成本函数

只涉及长期总成本、长期平均、长期边际

$$LAC=\frac{LTC}{Q}$$

$$LMC=\frac{\Delta LTC }{\Delta Q }$$

长期总成本曲线是尤数条短期总成本曲线的包络曲线,：长期中生产每一个特定产址花费的成本在所有短期成本中最低，而这种状态必然通过某一个短期内的最优选择来实现。

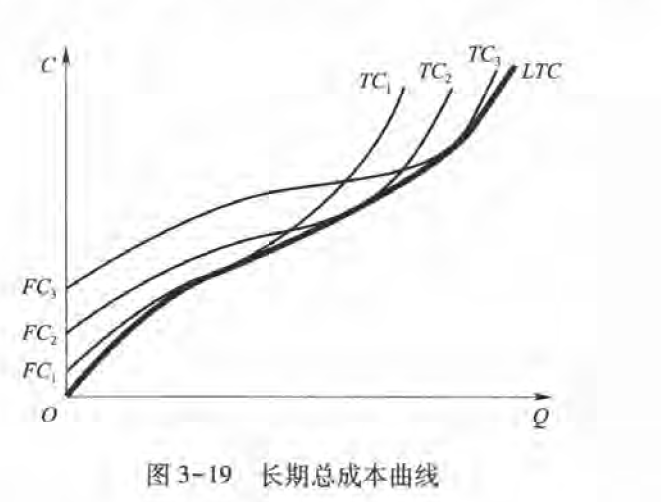
长期平均成本函数

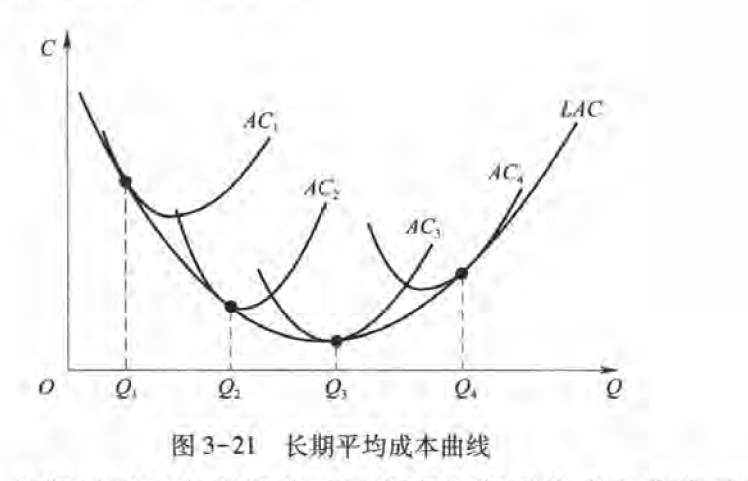
如果产措扩大一倍，而生产成本的增加小于一倍，则称企业的生产存在规模经济

$$\lambda^n Q=f(\lambda L,\lambda K)$$

$$f(\lambda L,\lambda K)=A(\lambda L)^\alpha(\lambda K)^\beta =\lambda^{\alpha+\beta}AL^\alpha K^\beta$$

$\alpha+\beta>1$则规模递增

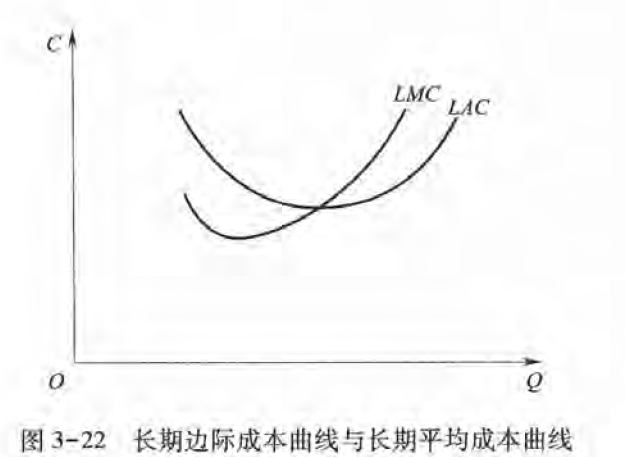
虽然长期边际成本曲线也为U形．但它并不是所有短期边际成本曲线的包络曲线